Materi 7.1 Sirkuit Kombinasi

[Menuju Akhir]

COMBINATIONAL CIRCUIT

DAFTAR ISI

1. Tujuan

2. Alat dan Bahan

3. Dasar Teori

4.Rangkaian

5.Prinsip Kerja

6.Video Simulasi

7. Example,problem,multiple choice

Link Download

1.Tujuan[Kembali]

• Memahami materi Circuit
• Memahami materi Combinational Circuit
• Mampu mengaplikasikan gambar pada materi kedalam proteus

2.Alat dan Bahan[Kembali]

Alat :

-Power Supply 

 

Power Supply atau dalam bahasa Indonesia disebut dengan Catu Daya adalah suatu alat listrik yang dapat menyediakan energi listrik untuk perangkat listrik ataupun elektronika lainnya.
-SPDT

SPDT (Single Pole Double Throw), merupakan golongan saklar yang memiliki 3 terminal. Jenis saklar ini dapat digunakan sebagai saklar pemilih. Contohnya, saklar pemilih tegangan input adaptor yaitu 110V atau 220V

- Logicstate

Gerbang Logika (Logic Gates) adalah sebuah entitas untuk melakukan pengolahan input-input yang berupa bilangan biner (hanya terdapat 2 kode bilangan biner yaitu, angka 1 dan 0) dengan menggunakan Teori Matematika Boolean sehingga dihasilkan sebuah sinyal output yang dapat digunakan untuk proses berikutnya.

- Logic Probe

Logic probe atau logic tester adalah alat yang biasa digunakan untuk menganalisa dan
mengecek status logika (High atau Low) yang keluar dari rangkaian digital.

Bahan :

- Gerbang AND

Gerbang logika AND adalah gerbang logika yang mempunyai masukan dua atau lebih serta mempunyai satu keluaran. Pada gerbang logika AND, masukan logikanya tinggi jika semua keluaran logikanya juga tinggi. Begitu pun sebaliknya, jika masukan logikanya rendah, maka keluaran logikanya akan rendah.

- Gerbang OR

Gerbang logika OR adalah gerbang logika yang sangat sederhana karena hanya memakai resistor dan transistor. Cara kerja pada gerbang logika OR berupa dua masukan daya listrik. Jika salah satu masukan diaktifkan, maka akan menghasilkan keluaran akan aktif juga.

- Gerbang NOT

Disebut juga sebagai Inverter (pembalik), Gerbang NOT memang memiliki konfigurasi terbalik. Ia dapat mengubah input 0 menjadi output 1, sedangkan input 0 akan menjadi output 1. Gerbang NOT juga sangat berbeda dengan gerbang lainnya, karena ia hanya mempunyai 1 input dan 1 output saja.

Gerbang NOT sering juga disebut sebagai rangkaian inventer (pembalik). Tugas rangkaian NOT (pembalik) ialah memberikan suatu keluaran yang tidak sama dengan masukan. Simbol logika untuk pembalik (inverter, rangkaian NOT) diperlihatkan pada gambar berikut

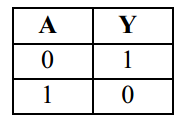
Simbol Logika Gerbang NOT

Alternatif Simbol Logika Gerbang NOT

Bila kita memasukkan pada masukan A suatu logis 1 maka akan kita peroleh logis yang berlawanan atau suatu logis 0 pada keluaran Y. Dapat kita katakan bahwa pembalik mengkomplemenkan atau membalik masukan. erikut tabel kebenaran untuk menjelaskan gerbang NOT

Tabel kebenaran Gerbang NOT

Perhatikan bila tegangan pada masukan adalah rendah, maka keluarannya adalah tinggi sebaliknya apabilah masukannya tinggi maka keluarannya adalah rendah. Seperti yang telah dijelaskan , keluaran selalu berlawanan dengan masukan. Tabel kebenaran tersebut juga memberikan karakteristik pembalik dari bentuk biner 0 dan 1.

3.Dasar Teori[Kembali]

COMBINATIONAL CIRCUIT

Sebuah sirkuit kombinasionaladalah salah satu di mana output setiap saat hanya bergantung pada kombinasi input saat ini pada titik waktu itu dengan total mengabaikan keadaan input di masa lalu. Gerbang logika adalah blok bangunan paling dasar dari logika kombinasional. Fungsi logis yang dilakukan oleh rangkaian
kombinasional sepenuhnya ditentukan oleh serangkaian ekspresi Boolean. Kategori lain dari rangkaian logika, yang disebut rangkaian logika sekuensial, terdiri dari gerbang logika dan elemen memori seperti flip-flop. Karena adanya elemen memori, output dalam rangkaian sekuensial tidak hanya bergantung pada input saat ini tetapi juga kondisi input sebelumnya. Blok bangunan dasar dari rangkaian logika sekuensial dijelaskan secara rinci dalam Bab 10 dan 11.

Gambar 7.1 menunjukkan representasi skema blok dari rangkaian kombinasional umum yang memiliki: n variabel masukan danMvariabel output atau hanya output. Karena jumlah variabel input adalah

 

n,ada 2nkemungkinan kombinasi bit pada input. Setiap output dapat dinyatakan dalam variabel input dengan ekspresi Boolean, dengan hasil bahwa sistem umum dari Gambar 7.1 dapat dinyatakan dengan Mekspresi Boolean. Sebagai ilustrasi, ekspresi Boolean yang menggambarkan fungsi gerbang OR/NOR empat masukan diberikan sebagai:

 

Y1 (OR Output) = A + B + C + D dan Y2 (NOR Output) = A' + B' + C' + D'

 Juga, masing-masing variabel input mungkin tersedia hanya sebagai input normal pada jalur input yang ditunjuk untuk tujuan tersebut. Dalam hal ini, masukan yang dilengkapi, jika diinginkan, dapat dibangkitkan dengan menggunakan inverter, seperti yang ditunjukkan pada Gambar 7.2(a), yang mengilustrasikan kasus fungsi kombinasional empat masukan, dua keluaran. Juga, masing-masing variabel input dapat muncul dalam dua kabel, satu mewakili literal normal dan yang lainnya mewakili yang dilengkapi, seperti yang ditunjukkan pada Gambar 7.2(b). Dalam sirkuit kombinasional, variabel input berasal dari sumber eksternal dan variabel output memberi makan tujuan eksternal. Baik sumber dan tujuan dalam sebagian besar kasus adalah register penyimpanan, dan ini

perangkat penyimpanan menyediakan baik output normal maupun yang dilengkapi dari variabel biner yang disimpan. Sebagai ilustrasi, Gambar 7.3 menunjukkan dua input sederhana (A, B-,empat keluaran (Y1,Y2,Y3,Y4) rangkaian logika kombinasional yang dijelaskan oleh ekspresi Boolean berikut:

Implementasi ekspresi Boolean ini membutuhkan input normal maupun input yang dilengkapi. Kebetulan, rangkaian kombinasional yang ditunjukkan adalah setengah-penambah-pengurang, dengan A dan B mewakili dua bit yang akan ditambahkan atau dikurangi dan Y1, Y2, Y3, Y4mewakili SUM,

PERBEDAAN, CARRY dan BORROW output masing-masing. Sirkuit penambah dan pengurang dibahas dalam Bagian 7.3, 7.4 dan 7.5.

Rangkaian simulasi[Kembali]

Prinsip kerja[Kembali]

1. Gerbang AND

(b) Simbol gerbang AND 

Tabel 1.1 Tabel Kebenaran Logika AND

Bisa dilihat diatas bahwa keluaran akan bernilai 1 jika semua nilai input adalah 1, dan jika salah satu atau lebih input ada yang bernilai nol maka output akan bernilai nol.

2. Gerbang OR

 Simbol gerbang OR 

Tabel 1.2 Tabel Kebenaran Logika OR

Bila dilihat dari rangkaian dasarnya maka didapat tabel kebenaran seperti di atas. Pada gerbang logika OR ini bisa dikatakan bahwa jika salah satu atau lebih input bernilai 1 maka output akan bernilai 1 . Nilai output bernilai 0 hanya pada jika nilai semua input bernilai 0. 

3. Inverter ( Gerbang NOT )

Simbol gerbang NOT Tabel 

1.3 Tabel Kebenaran Logika NOT

Gerbang NOT merupakan gerbang di mana keluarannya akan selalu berlawanan dengan masukannya. Bila pada masukan diberikan tegangan ,maka transistor akan jenuh dan keluaran akan bertegangan nol. Sedangkan bila pada masukannya diberi tegangan tertentu, maka transistor akan cut off, sehingga keluaran akan bertegangan tidak nol. 

Video simulasi[Kembali]

a. Video Rangkaian

b. Video Materi

Example,problem,multiple choice[Kembali]

 Example:

1. Desaign lah rangkaian atau sirkuit combinational logic yang menunjukkan operasi arithmatic dengan menambahkan 2 bit

2. Desaign lah rangkaian combinational logic yang menunjukkan operasi arithmatic dengan menambahkan 3 bits 

Problem

1. Sebuah 4-bit membawa penambah lookahead, yang menambahkan dua angka 4-bit, dirancang menggunakan gerbang AND, OR, NOT, NAND, NOR saja. Asumsikan bahwa semua input tersedia dalam bentuk komplemen dan tidak komplemen dan tundaan setiap gerbang adalah satu unit waktu, berapa tundaan propagasi keseluruhan penambah? Asumsikan bahwa jaringan carry telah diimplementasikan menggunakan logika AND-OR dua tingkat.

Jawab:

Biarkan input membawa ke penambah pertama dilambangkan dengan C1. Sekarang, untuk menghitung C2 kita membutuhkan = P1C1 + G1 = 4 level gerbang (P1 membutuhkan 2 level gerbang) untuk menghitung S1 kita membutuhkan = P1 XOR C1 = 2 + 2 = 4 level gerbang. Karena ini adalah carry look forward adder, komputasi C3 , S2 tidak harus menunggu pembawa output C2 dari adder sebelumnya karena C2, C3 dll akan dihitung pada waktu yang sama. Sekarang, S2 dihitung sebagai = P2 XOR C2 = P2.C2' + P2'.C2 = P2 (P1.C1 + G1 )' + P2' (P1.C1 + G1) [ perhatikan bahwa kita tidak menggunakan output carry dari penambah pertama C2 di mana saja di sini] yang dapat diimplementasikan menggunakan 4 level gerbang. juga C3 dapat dihitung dengan menggunakan 4 level gerbang dan seterusnya.Jadi penundaan propagasi keseluruhan adalah 4 level gerbang karena keluaran pada Si , Ci tersedia di masing-masing penambah penuh setelah 4 level gerbang = 4 unit waktu. Untuk memahaminya dengan lebih jelas, 

2. Perhatikan ALU yang ditunjukkan di bawah ini. Jika operan berada dalam representasi komplemen 2, operasi manakah di bawah ini yang dapat dilakukan dengan menyetel garis kontrol K dan C0 secara tepat saja (+ dan - masing-masing menunjukkan penambahan dan pengurangan) ?

Jawaban: A + B,  A - B, tetapi tidak A + 1

Kita dapat menetapkan nilai k dan c sebagai 0 atau 1 Dua hal yang perlu kita ketahui ---

• Jika kita mengambil xor dari sembarang angka dengan 1 kita mendapatkannya dalam bentuk komplemennya.
• Jika kita mengambil xor dari sembarang angka dengan 0 kita mendapatkan angka itu sendiri.

Jadi pada pengaturan k=1 kita bisa mendapatkan –B dan c akan bekerja seperti sinyal yang kita pilih, Seperti c=0 berarti menambah C=1 berarti kita mengurangi. Oleh karena itu dengan k=1 c=1 kita mendapatkan AB Dengan K=0 c=0 kita mendapatkan A +B Kita perlu b=1,c=0 atau b=0,c=1 untuk mendapatkan A+1 karena b tidak ditentukan sebelumnya, kita tidak bisa mendapatkan A+1 

Pilihan Ganda

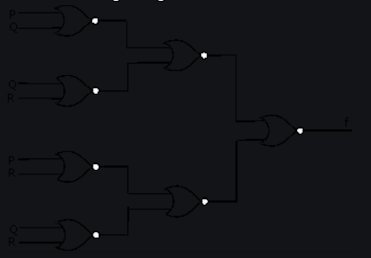
 1. Apa ekspresi Boolean untuk output f dari rangkaian logika kombinasional gerbang NOR yang diberikan di bawah ini?

A. (Q+R)'

B. (P+Q)'

C. (P+R)

D. (P+Q+R)'

Jawaban: A. (Q+R)'

Soal di atas mengandung gerbang NOR. Jika A dan B adalah dua input ke gerbang NOR, gerbang NOR memberikan (A+B)' sebagai output. Misalkan kita berikan nomor ke masing-masing gerbang untuk untuk mempermudah kita dalam menyelesaikannya. 

• Di kolom 1 ada 4 Gerbang NOR, dengan nomor  1 sampai 4 (atas ke bawah). 
• Di kolom ke-2 ada 2 Gerbang NOR, dengan nomor 5 dan 6 (atas ke bawah). 
• Di kolom 3 hanya ada 1 Gerbang NOR, dengan nomor  7.

• Gerbang bernomor 1 memberikan output sebagai: ( P + Q )' 
• Gerbang bernomor 2 memberikan output sebagai: ( Q + R )' 
• Gerbang bernomor 3 memberikan output sebagai: ( P + R )' 
• Gerbang bernomor 4 memberikan output sebagai: ( R + Q )' 
• Gerbang bernomor 5 memberikan output sebagai:

    (( P + Q )' + ( Q + R )')' 

    = ((P + Q)'' . ( Q + R )'') ( hukum De Morgan) 

    = (P + Q ). ( Q + R ) ( Hukum Idempoten, A'' = A) 

    = (PQ + PR + Q + QR ) = 

    (Q(1 + P + R) + PR) = Q + PR ( yang mana, 1 + " apa saja ekspresi boolean" = 1 )

    Demikian pula Gerbang bernomor 6 memberikan output sebagai: 

    R + PQ

                          

     Gerbang bernomor 7 memberikan output sebagai:

    ((Q + PR) + (R + PQ))'

    = (Q( 1+P) + R(1+P))'

    = (Q+R)'

2. Sebuah rangkaian mengeluarkan sebuah digit dalam bentuk 4 bit. 0 diwakili oleh 0000, 1 dengan 0001, ..., 9 dengan 1001. Kombinasional sirkuit dirancang menggunakan 4 bit tersebut sebagai input dan akan memberikan output 1 jika digitnya besar sama 5, dan akan beroutput 0 jika sebaliknya. Jika hanya gerbang AND, OR dan NOT yang dapat digunakan, berapa jumlah minimum gerbang yang diperlukan?

A. 2

B. 3

C. 4

D. 5

Jawaban: B. 3

Kita harus mendapatkan output 1 untuk nilai>=5. kita akan menggunkan tabel kebenaran untuk menyelesaikan soal tersebut

Di sini poin penting adalah bahwa kita perlu membuat pasangan dari 8 elemen menggunakan kondisi don't cares .jadi ekspresi akhirnya adalah

= A+BD+BC

= A+B(C+D) 

Oleh karena itu kita akan menggunakan dua gerbang OR dan satu gerbang AND sehingga total 3 gerbang. 

Link download [Kembali]

Download Rangkaian

Download Video Materi

Download Video Rangkaian

Download Datasheet SPDT

Download Datasheet AND 

Download Datasheet OR

Download Datasheet NOT

Download Materi

Download HTML

[Menuju Awal]